Racionalización de Fracciones con Radicales

Tratándose de radicales, el proceso de racionalización consiste en eliminar las raíces que se encuentran en el denominador de una fracción.

Dependiendo de las operaciones involucradas dentro de ese denominador pueden presentarse diversos casos:

a) caso en que el denominador contenga una raíz cuadrada, sin adiciones ni sustracciones.

Ejemplo:

Racionalizar: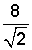 
Como regla general, amplificamos la fracción por el valor de este denominador, en este caso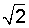  , de la siguiente manera:

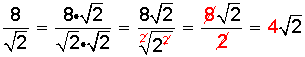
b) Caso en que el denominador contenga una raíz cuadrada, con adiciones o sustracciones.

Ejemplo:

Racionalizar: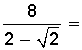 

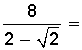
Igual que en el caso anterior, amplificamos la fracción, ahora por 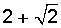 , para formar en el denominador una suma por su diferencia (corresponde al conjugado, que es la misma expresión pero con signo contrario), con lo cual dejamos la expresión en:

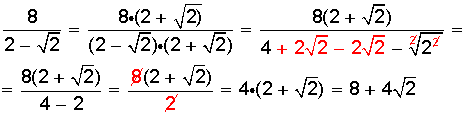
c) Caso en que hay una raíz cúbica en el denominador, sin adiciones o sustracciones.

Ejemplo:

Racionalizar: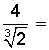 

En este caso amplificamos la fracción por 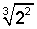 , para dejar la expresión del siguiente modo:

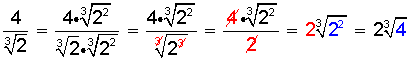
Racionalizar fracciones con radicales en el denominador sirve, entre otras aplicaciones, para ordenar de mayor a menor (para comparar) dichas fracciones.

Ejemplo:

Ordenar de menor a mayor las siguientes fracciones:

 

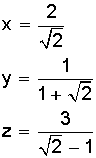
De acuerdo a lo aprendido arriba, racionalizamos cada una de las fracciones:

 

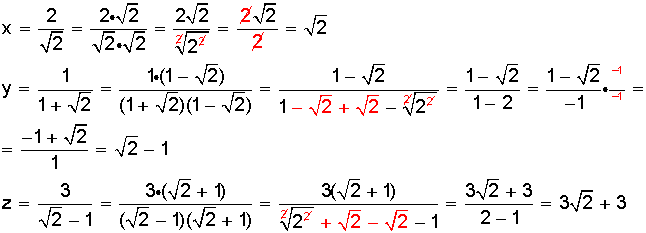
Hecho esto, podemos ordenar de mayor a menor: